ecuaciones no lineales
Solución de Ecuaciones No Lineales
Elena E. Álvarez Saiz
Red Educativa Digital Descartes.
Universidad de Cantabria
Título de la obra:
MÉTODOS NUMÉRICOS
Autores:
Elena E. Alvarez Saiz
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Primera Edición
LICENCIA
Tabla de contenido
Resolución aproximada de
ecuaciones escalares no lineales
Introducción
Imaginemos que consideramos la siguiente ecuación obtenida a partir de la segunda ley de Newton que permite obtener la velocidad de un paracaidista, $$v = {{g \cdot m} \over c}\left( {1 - {e^{ - {c \over m}t}}} \right)$$ donde la velocidad $v$ depende el tiempo, $t$ es el tiempo y es la variable independiente, $g$ es la constante de gravitación y $c$ el coeficiente de resistencia y $m$ la masa del paracaidista. ¿Cómo se podría obtener el coeficiente de resistencia del paracaidista con una masa dada, para alcanzar una velocidad determinada en un periodo establecido?
Si consideramos $$f\left( c \right) = {{g \cdot m} \over c}\left( {1 - {e^{ - {c \over m}t}}} \right) - v$$ el problema se corresponde con calcular el valor de $c$ de forma que $f(c)=0$. Vamos a ver en este capítulo cómo obtener el valor de la raíz o solucion de la función $f$.
En la mayoría de los casos, no será posible determinar la solución exacta de una ecuación de la forma $f(x)=0$ siendo $f$ una función real de variable real y se aplicará un algoritmo para determinar, en un número finito de pasos, un valor aproximado. Estos métodos de aproximación que, en general, son iterativos nos conducen a una solución a través de una sucesión $x_0, x_1, ..., x_k,...$ que converge al valor $x$ que es solución de la ecuación $f(x)=0$. Analizaremos también los problemas de convergencia y error que pueden presentarse.
Generalidades
A cualquier solución de la ecuación $f(x)=0$ se le llama cero o raíz de la funcion.
Sea $f$ una función continua en un intervalo abierto $I$, $\alpha$ un punto de $I$ y $m$ un número entero mayor o igual que 1. Se dice que $\alpha$ es un cero de $f$ de multiplicidad $m$ si
$$f\left( x \right) = {\left( {x - \alpha } \right)^m}q\left( x \right)\,\,\,\,\,\,\,\,x \ne \alpha $$
Se puede demostrar que si f es $C^m(I)$ y $\alpha$ es un punto de $I$, la función tiene un cero de multiplicidad $m$ en $\alpha$ si $$f(\alpha)=f'(\alpha)=...=f^{m-1}(\alpha)=0, f^{m}(\alpha) \ne 0$$
En cualquier proceso de cálculo de raíces de una ecuación se producen tres fases: localización, separación y aproximación.
En la fase de localización se busca conocer un intervalo donde se encuentra una o varias soluciones de la ecuación. La separación consiste en encontrar intervalos que contenga una sola raíz de la ecuación.
TEOREMA DE BOLZANO: Si $f$ es una función continua en $[a,b]$ de manera que $f(a)f(b) < 0$, entonces podemos asegurar que existe al menos un cero de la función en el intervalo [a,b].
El hecho de que sepamos que la función $f$ tiene un cero, no significa que sea único. Si añadimos condiciones adicionales, como por ejemplo la monotonía estrica de $f$ en un intervalo $I$, sí se podría garantizar que la solución de $f(x)=0$ es única en dicho intervalo.
En el caso de que la función sea derivable, si $f'(x)> 0$ en todo punto de $I$ la función es estrictamente creciente en I. Análogamente, si $f'(x)< 0$ en $I$ entonces es estrictamente decreciente.
En la fase de aproximación se construye una sucesión de valores que converja a la solución buscada. Normalmente se realiza mediante un método iterativo. En el caso de un método iterativo de un paso:- Se parte de un valor inicial $x_0$ que se supone suficientemente próximo a la solución buscada
- Se itera, es decir se obtiene mediante la fórmula $x_{k+1}=G(x_k)$ con $k \ge 0$
El método iterativo depende entonces de la función $G$ y del punto inicial $x_0$.
Las preguntas que se plantean son:
- si la sucesión es convergente (convergencia del método)
- si el límite de la sucesión es la solución de $f(x)=0$ que se pretende aproximar
- el número de iteraciones que hay que hacer para conseguir que el error que se cometa sea menor que una cantidad prefijada (velocidad de convergencia).
- cómo evoluciona el error al realizar las iteraciones (órden de convergencia que mide la velocidad con la que la sucesión se acerca a su límite).
Convergencia de un algoritmo
Se dice que un algoritmo converge globalmente, si la sucesión generada es convergente hacia una solución de la ecuación cualquiera que sea el punto inicial $x_0$ que tomemos. Cuando la solución converge hacia la solución únicamente si el punto $x_0$ pertenece a un cierto entorno de $x_0$, la convergencia es local.
No siempre es mejor considerar un algoritmo que converja globalmente, a veces, un algoritmo que sea localmente convergente, puede tener una "velocidad de convergencia" mayor si bien este tipo de algoritmos plantean la dificultad de cómo elegir el intervalo adecuado donde elegir $x_0$.
El método de aproximaciones sucesivas, que consiste en partir de un punto $x_0$ y calcular los demás términos de la sucesión $x_n$ de la forma $x_{n+1}=g(x_n)$, para calcular la raíz de $x=g(x)$, tiene una convergencia más lenta que el método de Newton que veremos en este capítulo y converge localmente.
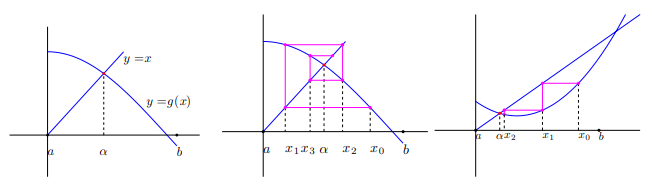
Se distinguen distintos tipos de convergencia que pasamos a definir.
Dada una sucesión de números reales, $\left\{ {x _k} \right\}_{k = 1}^\infty $, convergente hacia un punto $\overline x$, se dice que el orden o velocidad de convergencia es $p$, con $p \ge 1$ si existe una constante $C_p \ge 0$ tal que: $$\left| {{x_{k + 1}} - \overline x } \right| \le {C_p}{\left| {{x_k} - \overline x \,} \right|^p}$$ para todo $ k \ge k_0$ siendo $k_0$ entero.
- si $p$=1 y $C_p< 1$, la convergencia es lineal. Si $C_p \ge 1$, la convergencia es sublineal.
- si $p$=2, la convergencia es cuadrática.
- si $p$=3, la convergencia es cúbica.
Ejemplo Las sucesiones $a_n=1/n$, $b_n=1/n^3$, $c_n=1/2^n$ convergen linealmente al 0. La sucesion $d_n=3^{-2^n}$ converge cuadráticamente a 0.
Ejemplo Supongamos que $C_p=0.5$ y que $\left| {{x_k} - \overline x} \right| < 0.01$ entonces:
- Si $p=1$ $$\left| {{x_{k + 1}} - \overline x} \right| < C_p\left| {{x_{k}} - \overline x} \right| < 5 \cdot 10^{-1} \cdot 10^{-2}$$ $$ \left| {{x_{k + 2}} - \overline x} \right| < C_p \left| {{x_{k + 1}} - \overline x} \right|<5 \cdot 10^{-1} \cdot (5 \cdot 10^{-3}) =25 \cdot 10^{-4}$$
- Si $p=2$ $$\left| {{x_{k + 1}} - \overline x} \right| < C_p\left| {{x_{k}} - \overline x} \right|^2 < 5 \cdot 10^{-1} \cdot (10^{-2})^2 =5 \cdot 10^{-5}$$
Se dice que la sucesión converge superlinealmente, si existe una sucesión $\left\{ {{\varepsilon _k}} \right\}_{k = 1}^\infty $ convergente a 0 tal que $$\left| {{x_{k + 1}} - \bar x} \right| \le {\varepsilon _k}\left| {{x_k} - \bar x{\mkern 1mu} } \right|\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall k \ge 0$$
Observa que si la sucesión tiene una velocidad de convergencia $p$ mayor que 1 entonces converge superlinealmente.
Bastaría tomar $${\varepsilon _k} = {C_p}{\left| {{x_k} - \bar x{\mkern 1mu} } \right|^{p - 1}}\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall k \ge 0$$
Si $x_k$ converge superlinealmente a ${\bar x}$ entonces $$\mathop {\lim }\limits_{k \to \infty } {{\left| {{x_{k + 1}} - {x_k}{\mkern 1mu} } \right|} \over {\left| {{x_k} - \bar x{\mkern 1mu} } \right|}} = 1$$
Este resultado permite determinar un test de parada de las iteraciones cuando la convergencia es superlineal.
Una vez establecida la precisión que se quiere alcanzar, $\varepsilon > 0$, el test será: $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon$$ se compara así dos iteraciones consecutivas y se mira la coincidencia de dígitos que se considere (fijado por el valor de $\epsilon$).Método de Bisección
Aplicando el teorema de Bolzano, una forma sencilla de aproximar el cero de la función es dividir el intervalo en dos y elegir el subintervalo en el que se sigue produciendo el cambio de signo. Repitiendo este proceso se puede llegar a conseguir una aproximación de la solución de $f(x) = 0$ tan precisa como se desee.
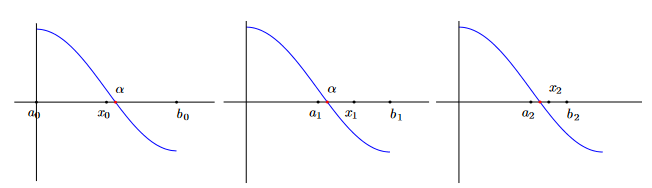 El método de bisección es un algoritmo utilizado para encontrar raíces de una función continua en un intervalo cerrado. Pasos a seguir:
El método de bisección es un algoritmo utilizado para encontrar raíces de una función continua en un intervalo cerrado. Pasos a seguir:
- Elige $[a, b]$ donde la función $f$ cambia de signo.
- Calcula el punto medio de $[a, b]$: $c = (a + b) / 2$.
- Si $f(a)$ y $f(c)$ tienen signos opuestos, la raíz está en el intervalo $[a, c]$; de lo contrario, está en $[c, b]$.
- Redefine el intervalo $[a, b]$ como $[a, c]$ si $f(a)$ y $f(c)$ tienen signos opuestos, o como $[c, b]$ si $f(c)$ y $f(b)$ tienen signos opuestos.
- Repite los pasos 2-4 hasta que $[a, b]$ sea lo suficientemente pequeño o se alcance una precisión deseada.
Iteración simple de punto fijo
Dada la ecuación $f(x)=0$, los pasos a seguir son:
- Se despeja $x$ como $x=g(x)$ buscando un punto fijo $\overline x$ de $g$, esto es un $\overline x$ cumpliendo $\overline x=g(\overline x)$.
- Partiendo de $x_0$ se busca la raíz haciendo iteraciones $$x_{k+1}=g(x_k), k=0,1,...$$ de manera que ${x_k}$ converja a $\overline x$
Veamos algunas condiciones suficientes (no necesarias) para que haya un punto fijo en un intervalo y condiciones suficientes de convergencia a un único punto fijo.
Sea $g$ continua en $[a,b]$ con $g(x)\in [a,b]$ para todo $x \in [a,b]$, entonces $g$ tiene un punto fijo en $[a,b]$.
Sea $g$ continua en $[a,b]$ con $g'$ en $(a,b)$ cumpliendo $$\left| {g'\left( x \right)} \right| \le L < 1\,\,\,\,\,\,\,\,para\,\,\,todo\,\,x \in \left( {a,b} \right)$$ Si $x_0$ es cualquier punto en $(a,b)$ entonces la solución $${x_{k + 1}} = g\left( {{x_k}} \right)\,\,\,\,\,\,k \ge 0$$ converge al único punto fijo en $[a,b]$.
Además, $$\left| {{x_{k + 1}} - \overline x} \right| \le {{{L^k}\left| {{x_1} - {x_o}} \right|} \over {1 - L}}\,\,\,\,\,\,k = 1,2,...$$
A veces se piensa que, si al utilizar el método del punto fijo $x_{k+1}$ y $x_k$ coinciden dentro de la exactitud especificada $\epsilon$, entonces se cumple que $\overline x \approx {x_{k+1}}$ con la misma exactitud. En el caso general, esta afirmación no es correcta. Si $g'(x)$ está próxima a la unidad, entonces la cantidad $\left| {{x_k} - \overline x} \right|$ puede ser grande, aún cuando $\left| {{x_{k+1}} - x_k} \right|$ sea extremadamente pequeña.
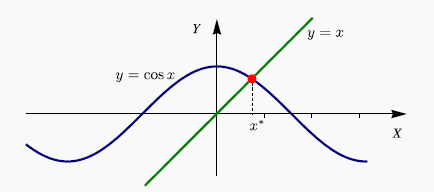
Ejemplo: Resolver $cos(x)-x=0$ considerando el siguiente algoritmo:
$$ {x_o} = 0.5 \,\,\, , \,\,\,\,\, {x_{k + 1}} = \cos \left( {{x_k}} \right)\,\,\,\,\,k,0,1,2,... $$A partir de la iteración 89 se estabiliza la sucesión obteniendo 0.739085133215161
Ejercicio 1 propuesto del tema 2.  . Calcular los ceros de $f(x)=x-e^{-x^2}$ en $[0,1]$ utilizando el método del punto fijo. Utiliza $g(x)=e^{-x^2}$ y $g(x)={-log(x)}^{-1/2}$. Empieza en el punto $0.5$. Realiza 100 iteraciones y analiza los resultados.
. Calcular los ceros de $f(x)=x-e^{-x^2}$ en $[0,1]$ utilizando el método del punto fijo. Utiliza $g(x)=e^{-x^2}$ y $g(x)={-log(x)}^{-1/2}$. Empieza en el punto $0.5$. Realiza 100 iteraciones y analiza los resultados.
Ejemplo: Acota las raíces de $p(x)=x^3+3x^2-1=0$ y determina cómo encontrar estas raíces mediante el método del punto fijo.
Se tiene que $p'(x)=3x^2+6x=3x(x+2)$ tiene dos ceros en el punto 0 y en -2. En el punto $(0,-1)$ hay un mínimo y en el punto $(-2,3)$ un máximo. Luego $p$ tiene tres raíces. Aislando estas tres raíces se tiene que están situadas en los intervalos [-3,-2], [-1,0], [0,1].
- En el intervalo [-3,-2], dividiendo por $x^2$ al ser $x$ distinto de 0, habría que calcular las raíces de $x+3-1/x^2=0$. Se puede considerar $g(x)=1/x^3-3$. En este caso la sucesión es convergente ya que $$\left| {g'\left( x \right)} \right| = \left| { - 2{x^{ - 3}}} \right| \le {1 \over 4} < 1$$
- En el intervalo [-1,0], la raíz a calcular será de la ecuación $x^2(x+3)=1$. Se puede considerar $g(x)=-\sqrt{(x+3)^{-1}}$ que aplica el intervalo $[-1,0]$ dentro del intervalo $[-1,0]$. En este caso $$\left| {g'\left( x \right)} \right| = \left| {{1 \over 2}{{\left( {x + 3} \right)}^{ - 3/2}}} \right| \le {1 \over {2 \cdot 2^{3/2}}} < 1$$
- En el intervalo $[0,1]$, la raíz a calcular será de la ecuación $x^2(x+3)=1$. Se puede considerar $g(x)=+\sqrt{(x+3)^{-1}}$ que aplica el intervalo $[0,1]$ dentro del intervalo $[0,1]$. En este caso $$\left| {g'\left( x \right)} \right| = \left| {{1 \over 2}{{\left( {x + 3} \right)}^{ - 3/2}}} \right| \le {1 \over {2 \cdot 3^{3/2}}} < 1$$
Método de Newton
Este método aproxima la solución de la ecuación $$f(x)=0$$ mediante una sucesión $x_k$ contruida, a partir de un valor inicial $x_0$, utilizando la expresión iterativa: $$x_{k+1} = x_k − \frac{f(x_k )}{ f'(x_k )}$$ La idea es, una vez obtenido $x_k$, obtener $x_{k+1}$ utilizando una aproximación lineal de $f(x)$ en el punto $x_k$. Se utiliza para ello la derivada $f$ en dicho punto: $$f(x) ≈ f(x_k )+f'(x_k)(x−x_k)$$ y se toma $x_{k+1}$ como la solución de la ecuación lineal $$f(x_k ) + f'(x _k )(x − x_k ) = 0$$
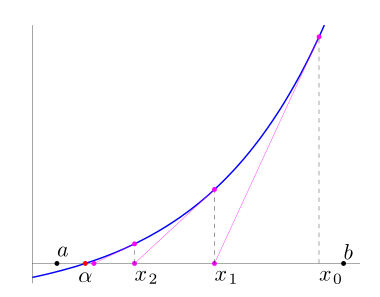
En la escena que se presenta a continuación, se muestra gráficamente la forma de proceder en el Método de Newton.
Tomando el punto inicial $x_0$ cercano a la solución, bajo ciertas condiciones sobre la función $f$, el método de Newton es convergente con orden de convergencia cuadrático (de orden 2).
Recordemos el siguiente teorema que permite, para una función continua, determinar si hay un cero.
Si $f$ es una función continua en $[a,b]$ de manera que $f(a)f(b) < 0$, entonces podemos asegurar que existe al menos un cero de la función en el intervalo [a,b].
Recordad también que el hecho de que sepamos que la función $f$ tiene un cero, no significa que sea único. Añadiendo condiciones adicionales, como por ejemplo la monotonía estrica, sí se podría garantizar que la solución es única.
Ejemplo. Busquemos la solución de la ecuación no lineal $$x-cos(x)=0$$
Tomamos el intervalo $[0,1]$ como el intervalo $[a,b]$ donde $f(a)f(b)$<$0$. Además, en ese intervalo la derivada es estrictamente positiva por lo que la función es creciente y solo hay un cero. Como punto $x_0$, consideramos el punto medio del intervalo $[0,1]$.
$x_0=0.5$
$x_1=x_0-\frac{x_0-cos(x_0)}{1+sen(x_0)}$ 0.755222417105636
$x_2=x_1-\frac{x_1-cos(x_1)}{1+sen(x_1)}$ 0.739141666149879
$x_3=x_2-\frac{x_2-cos(x_2)}{1+sen(x_2)}$ 0.739085133920807
$x_4=x_3-\frac{x_3-cos(x_3)}{1+sen(x_3)}$ 0.739085133215161
$x_5=x_4-\frac{x_4-cos(x_4)}{1+sen(x_4)}$ 0.739085133215161
El código Matlab a utilizar para encontrar la solución se muestra a continuación.
x=0.5
x=x-(x-cos(x))/(1+sin(x))
%A partir de la cuarta iteración se
%estabiliza el resultado
Observad que en este caso, se duplica, aproximadamentemente, la cantidad de decimales de cada iteracion (convergencia cuadrática).
Veamos a continuación algunos de los ejercicios propuestos como ejemplos.
Ejercicio 2d propuesto del tema 2. 
Vamos a calcular las raíces de $e^x+2^{-x}+2cos(x)=6$ en $[0,1]$
df=@(x) exp(x)-log(2)*2.^-x-2*sin(x)
%se busca un intervalo [a, b] con $f(a)f(b) < 0$
%Tomamos [1,2]
%Aplicamos el Método de Newton
x=1.5
x=x-f(x)/df(x)
%repetimos iteraciones hasta conseguir
%16 decimales
| $x_0$ | 1.500000000000000 | ||
| $x_1$ | 1.956489721124210 | $x_5$ | 1.829383601933849 |
| $x_2$ | 1.841533061042061 | $x_6$ | 1.829383601933849 |
| $x_3$ | 1.829506013203651 | ||
| $x_4$ | 1.829383614494166 |
Para calcular la diferencia entre dos iteraciones se podría utilizar el siguiente código Matlab:
df=@(x) exp(x)-2^-x*log(2)-2*sin(x)
x=1.5
x1=x-f(x)/df(x),error=abs(x-x1),x=x1;
df=@(x) exp(x)+2^-x*log(2)-2*sin(x)
k=1; x(k)=1.5
x(k+1)=x(k)-f(x(k))/df(x(k)),error=abs(x(k)-x(k+1)),k=k+1;
Ejercicio 4 propuesto del tema 2. 
%polyder deriva el polinomio
dp=polyder(p)
%polyval(p,a) evalúa el polinomio en a
%método de Newton
%intervalo [-4,-2]
polyval(p,-4);polyval(p,-2)
x=-3.25
x=x-polyval(p,x)/polyval(dp,x)
%repetimos iteracion, sol=-3.195823345445647
Si se repite con $x_0=1$ se puede observar que oscila entre negativo y positivo, no converge. Esto ocurre porque el método de Newton converge localmente.
Método de Newton combinado con la bisección
Supongamos que $f(a)f(b) < 0$. Se considera $a$ , $b$ y $x_0=\frac{a+b}{2}$.
En cada iteración se busca una nueva aproximación $x'$ y se actualizan $a$ y $b$ como se indica a continuación:
- Si $x'=x_0-\frac{f(x_0)}{f'(x_0}$ está en $[a,b]$ se acepta, en caso contrario se utiliza bisección, es decir, $x'=\frac{a+b}{2}$
- Se realiza $a'=x'$, $b'=b$ o $a'=a$, $b'=x'$, de manera que $f(a')f(b') < 0$
No se aplicará el método de Newton cuando el denominador $f'(x_k)$ sea muy pequeño (overflow), o mejor, cuando el cociente $\frac{f(x_k)}{f'(x_k)}$ sea muy grande. Es decir, no utilizaremos el método de Newton cuando $$|\frac{f(x_k)}{f'(x_k)}| > \frac{1}{\epsilon_M}$$ Esta última condición se implementa de la forma siguiente: $$|{f'(x_k)}| < {\epsilon_M} |{f(x_k)}|$$
Como tests de parada en las iteraciones, se considerarán:
- que la diferencia entre dos iteraciones consecutivas sea menor que un cierto valor $\epsilon$ $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon \,\,\,\,\text{error absoluto}$$ $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon |{x_{k+1}}| \,\,\,\,\text{error relativo}$$ combinando estos dos errores $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon \max \left\{ {1,\left| {{x_{k + 1}}} \right|} \right\}$$
- dado que se busca $f(x)=0$ se parará cuando $f(x_{k+1})$ sea pequeño, lo que comprobaremos con el test $$|f(x_{k+1})| < \epsilon_f$$ Para funciones sencillas un valor habitual es $$\varepsilon_f = \varepsilon _M^{3/4}$$
En el siguiente enlace puedes ver resumido el algoritmo.
Presentamos a continuación el algoritmo aplicado a un ejemplo:
Ejercicio 1d propuesto del tema 2.  . Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ en $[1,2]$.
. Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ en $[1,2]$.
f=@(x) exp(x)+2.^-x+2*cos(x)-6
df=@(x) exp(x)-log(2)*2.^-x-2*sin(x)
f(1)*f(2)
em=eps/2
a=1;b=2;fa=f(a);fb=f(b);x=(a+b)/2;fx=f(x);
[a b x],[fa fx fb]
ans =
-1.701113559804675 -1.023283135733256 0.806762425836365
Si $f(a) \cdot f(x) < 0$ se considera $[a,x]$, en caso contrario se considera $[x,b]$.
Iteración 1
a=x;fa=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m;[a x b],end
fx=f(x); [fa fx fb]
ans =
1.500000000000000 1.956489721124211 2.000000000000000
ans =
-1.023283135733256 0.579701373274924 0.806762425836365
Iteración 2
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[fa fx fb]
ans =
1.500000000000000 1.841533061042061 1.956489721124211
ans =
-1.023283135733256 0.050340951614865 0.579701373274924
Iteración 3
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
ans =
1.500000000000000 1.829506013203651 1.841533061042061
ans =
-1.023283135733256 0.000502121322591 0.050340951614865
Iteración 4
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
ans =
1.500000000000000 1.829383614494166 1.829506013203651
ans =
-1.023283135733256 0.000000051516139 0.000502121322591
Iteración 5
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
ans =
1.500000000000000 1.829383601933849 1.829383614494166
ans =
-1.023283135733256 0.000000000000001 0.000000051516139
Ejercicio 1d propuesto del tema 2.  . Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ que se encuentra entre $[-3,-2]$.
. Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ que se encuentra entre $[-3,-2]$.
df=@(x) exp(x)-log(2)*2^(-x)-2*sin(x)
f(-3)*f(-2)
a=-3;fa=f(a);b=-2;fb=f(b);x=(a+b)/2;fx=f(x),
[a x b],[f(a) f(x) f(b)]
-3.000000000000000 -2.500000000000000 -2.000000000000000 ans =
0.069802075166974 -1.863347982977588 -2.696958389857672
Iteración 1
if abs(dfx)>em*abs(fx),x=x-fx/dfx;if a$<$=x & b$>$=x, disp('Se aplica Newton'),
[a x b],fx=f(x);end,end
%Si no está en [a,b] o no se
%cumple abs(dfx)>em*abs(fx)
%aplicamos bisección
x=(a+b)/2;fx=f(x);[a x b],[fa fx fb]
ans =
-3.000000000000000 -2.750000000000000 -2.500000000000000
ans =
0.069802075166974 -1.057505574028503 -1.863347982977588
Iteración 2 Bisección
-3.000000000000000 -2.875000000000000 -2.750000000000000
ans =
0.069802075166974 -0.536899807501486 -1.057505574028503
Iteración 3 Newton
-3.000000000000000 -2.994267548648236 -2.875000000000000
ans =
0.069802075166974 0.040014356224199 -0.536899807501486
Iteración 4 Newton
-2.994267548648236 -2.986542066999646 -2.875000000000000
ans =
0.040014356224199 0.000174552940576 -0.536899807501486
Iteración 5 Newton
-2.986542066999646 -2.986508070038639 -2.875000000000000
ans =
0.000174552940576 0.000000003371666 -0.536899807501486
Iteración 6: Newton
-2.986508070038639 -2.986508069381928 -2.875000000000000
ans =
0.000000003371666 0 -0.536899807501486
El método de Newton tiene el problema de que podría darse “overflow” si se divide por un número muy pequeño, o converger a otra raíz (no a la raíz que se busca) o incluso no converger. Además, al requerir la derivada de la función podría ser difícil de obtener en el caso de ciertas funciones como las definidas por integrales o por series infinitas por ejemplo.
Método de la secante
Iniciado con dos aproximaciones iniciales $x_o$ y $x_1$, en el paso $k+1$, $x_{k+1}$ se calcula usando $x_k$ y $x_{k-1}$ como la intersección con el eje X de la recta secante, que pasa por los puntos $(x_{k-1}, f(x_{k-1})$ y $(x_{k}, f(x_{k})$
La ecuación de la recta secante es $$y = f\left( {{x_k}} \right) + {m_k}\left( {x - {x_k}} \right)\,\,\,\,\,\,\,\,\,\,\,\,{m_k} = {{f\left( {{x_k}} \right) - f\left( {{x_{k - 1}}} \right)} \over {{x_k} - {x_{k - 1}}}}$$
El método proporciona $x_{k+1}$ como solución de $$0 = f\left( {{x_k}} \right) + {m_k}\left( {x - {x_k}} \right)$$ Es decir, $${x_{k + 1}} = {x_k} - {{f\left( {{x_k}} \right)} \over {{m_k}}}\,\,\,\,\,\,\,\,\,\,\,\,{m_k} = {{f\left( {{x_k}} \right) - f\left( {{x_{k - 1}}} \right)} \over {{x_k} - {x_{k - 1}}}}$$
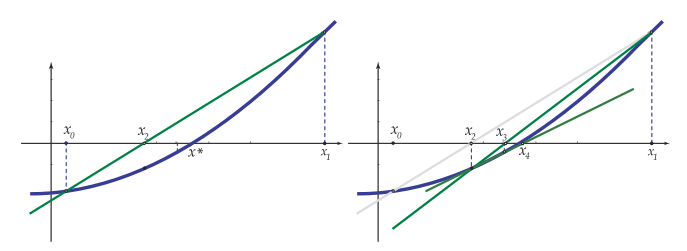
Método de la secante-bisección
De la misma forma que el método de Newton, resulta muy conveniente combinar programar este método combinado con el método de la bisección
Se partirá de un intervalo $[a,b]$ donde $f(a)f(b)< 0$. Se toma $x_0=a$ y $x_1=b$.
En cada iteración, se parte de un intervalo $[a,b]$ y se busca una nueva aproximación $x_2$ actualizando de nuevo $a$ y $b$ como se indica a continuación:
- Si $x_2=x_1-\frac{f(x_1)}{m_1}$ está en $[a,b]$ se acepta, en caso contrario se utiliza bisección, es decir, $x_2=\frac{a+b}{2}$
- Se modifica el intervalo $[a,b]$ tomando $a=x_2$, o $b=x_2$, de manera que en el nuevo intervalo se verifique $f(a)f(b) < 0$
Tampoco se aplicará el método de la secante cuando el denominador $m_k$ sea muy pequeño. Esta última condición se implementa de la forma siguiente: $$|{m_k}| > {\epsilon_M} |{f(x_k)}|$$
Los test de parada a utilizar son los mismos que en el caso del método Newton-Bisección.
Ejercicio 10 propuesto del tema 2. 
f=@(x) erf(x)-0.5
f(0)*f(1)
a=0;b=1;fa=f(a);fb=f(b);x0=a;fx0=fa;x1=b;fx1=fb;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1);x=x1-fx1/m;end
[a x b],[fa fx fb]
%Se comprueba que está en [a,b]
Iteración 1:
0 0.593330401707401 1.000000000000000
ans =
-0.500000000000000 0.098584503929305 0.342700792949715
Iteración 2:
0 0.429099981968989 0.593330401707401
ans =
-0.500000000000000 -0.043957753989566 0.098584503929305
Iteración 3:
0.429099981968989 0.479746018406641 0.593330401707401
ans =
-0.043957753989566 0.002522030582461 0.098584503929305
Iteración 4:
0.429099981968989 0.476997923639157 0.479746018406641
ans =
-0.043957753989566 0.000055407570768 0.002522030582461
Iteración 5:
0.476936193389100 0.476936276206905 0.476997923639157
ans =
Iteración 6:
ans =
1.0e-04 * -0.000744351095761 0.000000021886937 0.554075707681623
Iteración 7:
0.476936193389100 0.476936276204470 0.476936276206905
ans =
1.0e-07 * -0.744351095760543 0 0.000021886936707
Ejercicio 12 propuesto del tema 2. 
%f(x)=det(A(x)+2I)
f=@(x) det([x+2 2 -3 5 0 x^2;1 3 1 1 1 1;0 x x+2 0 5 -2;1 -1 1 1 2*x 0;1 0 1 0 (x^2)+2 -2;0 0 1 0 cos(x) -x+2])
%Buscamos cambios de signo
% f(0)$<$0
% f(1)$<$0
% f(2)$>$0
% f(3)$<$0
% f(4)$<$0
% f(5)$<$0
% f(-1)$<$0
% f(-2)$<$0
Aplicamos el método de la secante dada la dificultad de calcular la derivada.
a=1;b=2;fa=f(a);fb=f(b);x0=a;x1=b;fx0=fa;fx1=fb;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1),x=x1-fx1/m;end
[a x b],fx=f(x);[fa fx fb]
%Hay que comprobar que el punto
%quede dentro del intervalo
%Se itera hasta que converja
ans =
1.182136884006676
Cálculo de las raíces de un polinomio
En este apartado, nos ocuparemos de encontrar todas las soluciones (reales y complejas) de un polinomio, es decir, resolveremos todas las soluciones de $${a_o} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n} = 0$$
- Teorema Fundamental del Álgebra: Un polinomio de grado $n$ tiene exactamente $n$ raíces en el conjunto de los números complejos, donde cada una de ellas debe contarse con su multiplicidad.
- Si un polinomio tiene coeficientes reales, siempre que tenga una raiz compleja no real, también tendrá su conjugada.
- Si $p\left( x \right) = {a_o} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}$, todas las raíces satisfacen $${{\left| {{a_0}} \right|} \over {b + \left| {{a_0}} \right|}} \le \overline x \le 1 + {c \over {\left| {{a_n}} \right|}}\,\,\,\,$$ siendo $$b = \max \left\{ {\left| {{a_1}} \right|,\,\,\left| {{a_2}} \right|,...,\left| {{a_n}} \right|} \right\}$$ $$c = \max \left\{ {\left| {{a_0}} \right|,\,\,\left| {{a_1}} \right|,...,\left| {{a_{n - 1}}} \right|} \right\}$$
Aunque inicialmente se había descrito el método de Newton para calcular las soluciones de una ecuación $f(x)=0$ con $f$ función real de variable real, el método también es válido para encontrar soluciones de funciones complejas. Además, la derivada de un polinomio es fácilmente calculable por lo que el método de Newton resulta adecuado para calcular las raíces de un polinomio.
Sin embargo, nos planteamos a la hora de calcular todas las raíces del polinomio, si una vez obtenida una raíz, $\alpha$, y querer encontrar otra, ¿cómo se podría evitar que el método de Newton vuelva a converger a la raíz ya calculada?
Una primera idea sería elegir otro punto de inicio, sin embargo, esto no garantizaría que el método deba converger a otra raíz.
Otra posibilidad, podría ser considerar el polinomio resultado de dividir $p(x)$ entre $x-\alpha$ y aplicar el método de Newton a este nuevo polinomio. Este método, conocico como deflacción, presenta también problemas:
- La operación de división conlleva errores de redondeo.
- El método de Newton nos devuelve una aproximación de la raíz exacta, $\alpha *$ por lo que el cociente $\frac{p(x)}{x-\alpha}$ no coincide con $\frac{p(x)}{x-\alpha *}$ y, en consecuencia, no tienen por qué tener las mismas raíces.
Dado que el hecho de que dos polinomiostengan coeficientes muy próximos no implica que tengan las mismas raíces (por ejemplo, basta considerar $p(x)=x^2+1.99x+1.01$ y $q(x)=x^2+2x+1$). El método alternativo a utilizar es el Método de Maehly.
Se puede ver que $${{{f_m}\left( x \right)} \over {f{'_m}\left( x \right)}} = {{p\left( x \right)} \over {p'\left( x \right) - p\left( x \right)\sum\limits_{j = 1}^m {{1 \over {x - {\alpha _j}}}} }}$$
Puedes descargar el fichero itraiz.m que realiza una iteración del método de Maehly.
Hay que tener en cuenta que
- A la hora de calcullar la primera raiz, el algoritmo se reduce a aplicar el método de Newton al polinomio: $$\begin{aligned} & {x_o} \in \mathbb C \\ & x_{k + 1} = {x_k} - \frac{p(x_k)} {p'(x_k)} \,\,\,\,\,\, k \ge 0 \end{aligned}$$
- Si los coeficientes del polinomio son todos reales y $x_0$ es real, la sucesion ${x_k}$ será de números reales y no podrá converger a una raíz compleja. Por lo tanto, deberá tomarse $x_0$ complejo si se quiere encontrar una raíz compleja.
El método de Newton converge cuadráticamente hacia una raíz $\overline x$ si $p'(\overline x)\ne0$. Si se observa que los valores de $x_k$ convergen pero lentamente, puede deberse a que se está aproximando a una raíz múltiple o hay raíces muy próximas. En este caso se aplica el método de Newton a la derivada del polinomio comenzando en el último punto $x_k$ calculado en las iteraciones sobre $p$.
Si la convergencia siguiera siendo lenta, entonces se aplicaría el método de Newton a la segunda derivada. Si calculamos una raíz $\alpha$ de $p'(x)$ (o de derivadas sucesivas de p) y observamos que $$\left| {p\left( \alpha \right)} \right| \gg \left| {p'\left( \alpha \right)} \right|$$ entonces debemos concluir que $\alpha$ no es raíz de $p$, lo que ocurre es que $p$ posee dos o más raíces muy próximas.
- Si el polinomio tiene coeficientes reales y $\alpha=a+bi$ es una raiz compleja entonces su conjugada $\overline \alpha = a - bi$ también es raíz del polinomio. Además, si $\alpha$ tuviera multiplicidad $m$, entonces $\overline \alpha$ tendría la misma multiplicidad.
En caso contrario, tendremos que $\alpha$ es una raíz doble de $p$ (o de multiplicidad $j+1$ si $$p\left( \alpha \right),\,\,p'\left( \alpha \right)...{p^{(j}}\left( \alpha \right)$$ toman valores muy pequeños.
En el caso de que haya raíces próximas entonces la convergencia será lenta y, en general, no podremos obtener una precisión alta en la solución.
Ejercicio 9 apartado b propuesto del tema 2. 
dp=polyder(p)
v=[]
x=i
format long
x=itraiz(p,dp,v,x)
%Se hacen iteraciones hasta encontrar x
-1.056847723228969 + 0.262522264027478i
polyval(p,x)
x=i;x=itraiz (p,dp,v,x) x=
-0.059269229873907 + 2.202319797999819i
polyval(p,x)
x=i;x=itraiz (p,dp,v,x)
2.063556841734012
polyval(p,x)
Se obtienen así las 7 raíces
-1.056847723228969 + 0.262522264027478i
-1.056847723228969 - 0.262522264027478i
-1.540661467764130 + 1.474052474547216i
-1.540661467764130 - 1.474052474547216i
-0.059269229873907 + 2.202319797999819i
-0.059269229873907 - 2.202319797999819i
2.063556841734012 + 0.000000000000000i
Ejercicio 9 apartado f propuesto del tema 2. 
Ejercicio 9 apartado e propuesto del tema 2. 
Octave online
Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.
Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.