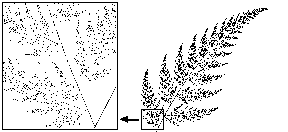
Standard choice.
The classical mathematical concepts and methods are concerned with smooth objects, ignoring irregular sets. For example, the concept of derivative allows us to analyze smooth curves and surfaces, characterizing their properties. However, in recent years it has been shown that many nonlinear phenomena are so complicated and irregular that they cannot be modeled well using these classical techniques. Examples of these phenomena appear, for instance, in problems as varied as the growth and decline of populations, prediction of the weather, fluid turbulence, and economical series (see, for example, Peitgen et al. (1993)). The development of fractal geometry (Mandelbrot 1982) provides us with rigurous concepts and practical techniques suitable for the mathematical formulation and analysis of irregular processes. For example, the fractal dimension of strange attractors associated with chaotic dynamical systems gives a valuable information about the irregular evolution observed in such systems.
With the aim of giving some insight in such problems, several methods for fractal modeling and generation have been introduced in the last two decades. All these methods help us to understand many interesting nonlinear phenomena recently appeared, like those associated with chaotic dynamical systems. Among these methods, the Iterated Function Systems (IFS) models, popularized by Barnsley in the 80's (Barnsley 1988), are very useful for modeling and generating self-similar fractals. These models are particularly interesting due to its mathematical soundness and simplicity, since an IFS fractal is defined by a finite number of linear transformations {w1,...,wN}. Thus, a minimum set of input data is required. IFS models have been successfully applied in many disciplines as, for example, in the field of computer graphics, finding a huge number of applications in different areas such as artificial landscape modeling, visual trainning systems, image compressing, etc. (for further details see (Fisher 1995)).
The term multifractal is applied when many fractal subsets with different scaling properties coexist simultaneously. In this sense, a measure defined on a fractal may have a multifractal character. The irregularity of this measure contains much information about the system that can be conveniently analyzed using multifractal theory. The main objective of the multifractal analysis of a measure m defined on a fractal set, S, is characterizing the dimensions and the structure associated with the sets S(a), as a function of the singularities a (for further information see, for example, (Falconer 1990)). where B(x,e) is the e-radio ball with centered at x. Each of the singularities a determine a subset of the fractal, S(a), with a characteristic scaling property which is given by the corresponding fractal dimension d(a). In the case of measures generated generated with the chaos game algorithm, it can be shown that all the singularities are of the form where x1+...+xn=1, being the associated dimension
A practical application of this multifractal analysis is related to the rendering efficiency of the probabilistic algorithm to reder the fractal image given by an IFS model (also known as chaos game). This algorithm works by attaching real weights pi to each of the transformations in the IFS, such that p1+...+pN = 1. Picking an initial point, one of the mappings in the set {w1,...,wN} is chosen at random using the weigths {p1,...,pN}. The selected map is then applied to generate a new point, and the same process is repeated again with the new point obtaining, as a result of this iterative process, a sequence of points. The sequence obtained using this stochastic process converge to the fractal as the number of points increases. This algorithm is known as probabilistic algorithm or "chaos game" (see for example [Barnsley 1988]).Regarding the problem of the choice of probabilities for generating the fractal attractor of an IFS applying the "chaos game", the standard criterion for this choice is the proportionality with respect to the contractive factor (see, for example, M. F. Barnsley (1990) "Fractals Everywhere", Academic Press, pag. 85). The efficiency of this algorithm to render the attractor of an IFS using a set of probabilities {p1,...,pN} can be related to the spectrum of singularities of the multifractal measure associated with the corresponding IFSP. Thus, we use the multifractal analysis introduced in this paper to obtain the most efficient choice of the probabilities.
For example, consider the fern IFS given by the mappings
w1(x,y)=(0.81x+0.07y+0.12,-0.04x+0.84y+0.195),
w2(x,y)=(0.18x-0.25y+0.12,0.27x+0.23y+0.02),
w3(x,y)=(0.19x+0.275y+0.16,0.238x-0.14y+0.12),
w4(x,y)=0.0235x+0.087y+0.11,0.045x+0.1666y).
The figures below show the fractal images generated by the "chaos game" algorithm using the standard probabilities (p1=0.753, p2=0.123, p3=0.104, p4=0.020)
Standard choice.
and the probabilities obtained based on the multifractal structure of the resulting IFSP (p1=0.701, p2=0.150, p3=0.129, p4=0.020).
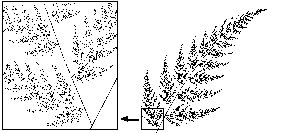Our proposal.
In both cases the same number of iterations is performed.
The difference can be established visually.