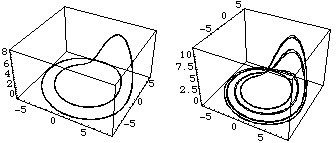
In the last two decades many researchers have studied the behavior of many non-linear dynamical systems (see e.g. Jackson [1991]), including the appearance of deterministic chaos, that is characterized by the sensitive dependence on the initial conditions of a trajectory of the system. In the case of dissipative systems described through nonlinear ordinary differential equations and exhibiting deterministic chaos, the system evolves in phase space over a fractal structure called strange or chaotic attractor, that consists of a continuous stretching and folding process. Deterministic chaos is usually associated with wild oscillations in the variables that may be inconvenient in practical applications of the systems exhibiting these features and, thus, for many applications one would like the system to have a more regular behavior. Although a chaotic system may appear at first sight to exhibit stochastic behavior, its deterministic nature implies that it has some regularity in its inner structure. In fact, it has been shown [Cvitanovic, 1988] that a chaotic system may bee seen as the superposition of a large number of unstable periodic orbits (also called cycles). The idea of controlling chaos consists precisely in the stabilization of any of these orbits embedded in the strange attractor.
For example, the Rossler model is given by the following set of coupled differential equations and that exhibit deterministic chaos for certain values of the parameters [Rossler, 1976]
x'=-y - z
y'=x + a y
z'=b + z (x - c)
For example, for the values of the parameters a=0.2, b=0.2, and c=4.6 the system exhibits deterministic chaos. Fixing a and b to these values and considering c as the control parameter the model exhibits a Feigenbaum's period-doubling route to chaos, a universal scenario for chaos transition.
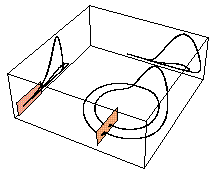
Different classes of methods have been suggested in the literature for the suppression of chaotic behavior in non-linear systems. Within the framework of the original method due to Ott, Grebogi, and Yorke (OGY) [Ott et al. 1990], one uses a Poincare section of the system in order to reduce in one the dimensionality of the system, skipping the direction having Lyapunov exponent equal to zero. The fixed point of the return map corresponding to the desired orbit of the flow is then stabilized by means of a linear approximation in a trust ball around this point. In practice, this is carried out by exploiting the saddle character of these unstable periodic orbits, namely by making the trajectory to lie at each crossing on the stable direction, called stable manifold, of the target orbit. In another set of methods one uses different ways of perturbing the sysems parameters to achieve chaos suppression (see, for example, [Lima and Pettini, 1990], [Pyragas, 1992]).
The above mentioned methods work by applying perturbations on some system parameter. However, in a recent contribution [Matías and Guémez, 1994] a new method that operates by performing changes in the system variables has been suggested and applied to the case of some typical three-dimensional flows, although its capabilities to deal with maps, {\it i.e.\ }difference equations, have been also proved. This method applies perturbations on the system variables in two different forms. In the first method the pulses are proportional x -> x (1 + p). The second method tries to offer a simpler alternative through the use of additive pulses, x -> x +p, where p is the pulses strength. A series of paper analyzed from both theoretical and practical points of view the preformance of this method, and the similarities with other algorithms for controlling chaos both in discrete and continous dynamical systems [Guémez, Gutiérrez, Iglesias, and Matías]. For example, the above chaotic Rossler system can be switched from chaotic to different period behavior following the period-doubling route to chaos.
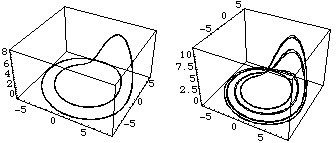
This control method can also be applied to the logistic map:
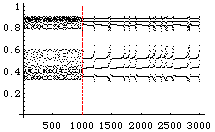
x(n+1) = r x(n) (1-x(n)),
switching the system to some periodic orbit
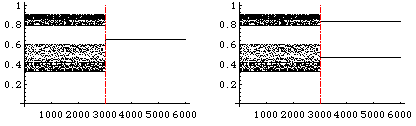
or to an intermitency region.