Algoritmos voraces y MSTs

1 Algoritmos voraces

Los algoritmos voraces son algoritmos que tratan resolver problemas siempre eligiendo la mejor opción.

2 Minimum Spanning Trees

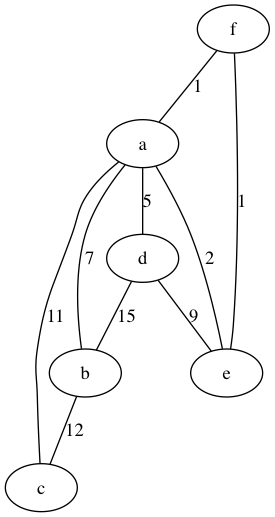
grafo.png

Figura 1: Grafo con pesos

3 Minimum Spanning Trees

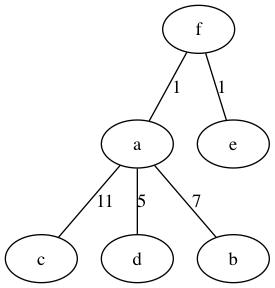
mst.png

Figura 2: Arbol de peso mínimo

4 El algoritmo de Kruskal

  • Problema: Encontrar un árbol de peso mínimo.
  • Heurística: Añadir la arista de menor peso que no genere ciclos
  • Idea: para comprobar si dos nodos están unidos, simplemente hay que utilizar la función conectados.

5 El algoritmo de Kruskal

  def Kruskal(G):
    X = set()  #Conjunto con las aristas del arbol
    G.E.sort() #Ordenar las aristas por el peso
    for (u,v) in G.E:
      if not conectados(u,v):
        X.add((u,v))
        unir(u,v)

6 Traza del algoritmo de Kruskal

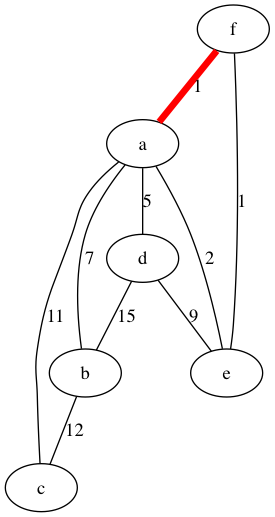
traza0.png

Figura 3: Añadimos la arista de f a a.

7 Traza del algoritmo de Kruskal

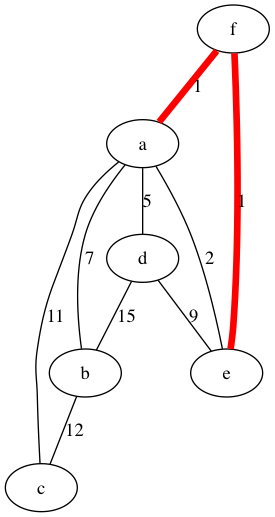
traza1.png

Figura 4: Añadimos la arista de f a e

8 Definición de corte

Un corte en un grafo es una partición en dos conjuntos \((S,T)\) de sus vértices. El conjunto asociado a un corte son las aristas que unen vértices de \(S\) con vértices de \(T\).

9 Ejemplo de corte

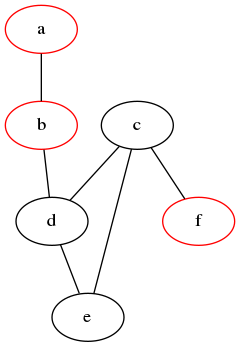
corte.png

Figura 5: Ejemplo de corte

10 Propiedad del corte

Dado un corte \(S,T\), entonces la arista de mínimo peso que une un nodo cualquiera de \(S\) con un nodo de \(T\) pertenece a algún minimum spanning tree.

11 El algoritmo de Prim

  • Empezar por un nodo.
  • Ir generando un arbol añadiendo arista por arista.
  • Elegir la arista del mínimo peso pero de forma que se forme un árbol.

12 El algoritmo de Prim

  def Prim(G,a):
  X = set()
  Corte = set(a)
  mientras X tenga menos de |G.V|-1:
     Añadir la arista minima asociada a Corte a X.
     Añadir el nodo destino de la arista a Corte.

13 Traza del algoritmo de Prim

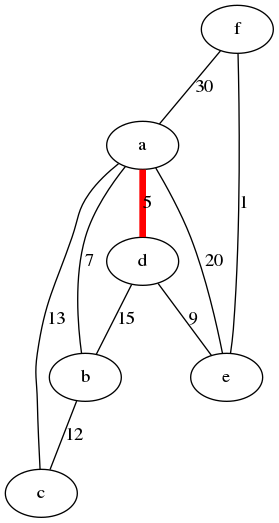
traza4.png

Figura 6: Traza del algoritmo de Prim empezando en a

14 Traza del algoritmo de Prim

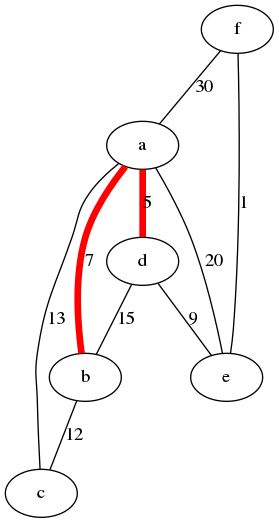
traza5.png

Figura 7: Traza del algoritmo de Prim empezando en a