Quick Union y Quick Find

1 Dynamic connectivity

Dado un conjunto de N objetos (vértices), se definen dos operaciones:

  • Unir dos objetos
  • Comprobar si dos objetos están unidos por un camino (conectados)

Dos objetos se dicen que son adyacentes si están unidos.

2 Definición de grafo no dirigido

Un grafo es un par (V,E), donde V es un conjunto de vértices y E es una lista de pares nodos que están unidos.

3 Implementación de grafos

La implementación más eficiente de un grafo es utilizando listas de adyacencia:

  • Cada nodo se representa por un entero.
  • El grafo se representa por un array de tamaño N, donde en cada posición hay una lista con los nodos adyacentes al dado.

4 Dynamic connectivity

grafo.png

5 Dynamic connectivity

unir(0,2);

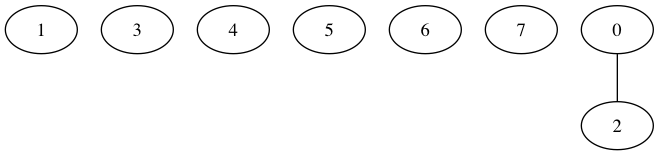
grafo1.png

6 Dynamic connectivity

unir(0,2);unir(1,7);

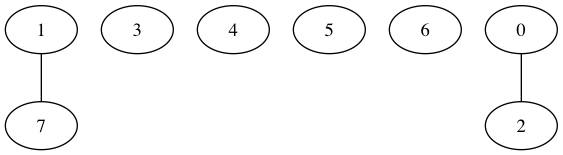
grafo2.png

7 Dynamic connectivity

unir(0,2);  unir(1,7);  unir(4,5);  unir(7,3);
unir(2,3);  unir(0,4);  conectados(0,3);

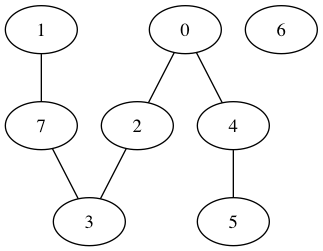
grafo3.png

8 Pregunta

Vamos a hacer una pregunta para responder en la encuesta:

  • Tenéis cinco minutos para responder.
  • Si no sabéis la respuesta, elegid una al azar.
  • Después de cinco minutos preguntaré a personas al azar SIN CORREGIR.
  • Si hay disparidad de opiniones, tendréis cinco minutos más donde PODÉIS PREGUNTAR A COMPAÑEROS.
  • Después, volveré a preguntar y resolveremos.

9 Pregunta

  • ¿Están conectados los nodos 0 y 7?
  • ¿Están conectados los nodos 6 y 1?
  • Dar un par de nodos, separados por una coma, que hay que unir para que 0 y 6 estén conectados pero no sean adyacentes.

grafo3.png

10 ¿Por qué necesitamos algoritmos?

grafo_grande.png

11 ¿Por qué necesitamos algoritmos?

  • Amigos en una red social.
  • Pixels en una fotografía.
  • Transistores en un circuito digital.
  • Pintar una región en una foto.

12 La relación de conexión

Se cumplen las siguientes propiedades:

  • Un nodo p siempre está conectado consigo mismo (propiedad reflexiva).
  • Si p está conectado con q entonces q está conectado con p (propiedad simétrica).
  • Si p está conectado con q y q está conectado con r entonces, p esta conectado con r (propiedad transitiva).

Los elementos que están relacionados, forman una clase de equivalencia, para la relación de estar conectados, se llaman las componentes conexas.

13 Ejemplo

grafo3.png

Las componentes conexas en este grafo son \[\{0,1,2,3,4,5,7\}, \{6\}.\]

14 Objetivo

Conseguir una estructura de forma que podamos calcular eficientemente las componentes conexas de un grafo. Hay que tener en cuenta que:

  • El número de llamadas a la función unir puede ser muy grande.
  • El número de llamadas a la función conectados puede ser muy grande.
  • Se pueden intercalar llamadas de una y otra función.

15 Estructura de datos

Vamos a utilizar un array de enteros id:

  • El tamaño del array es n.
  • Dos nodos p, q están en la misma componente si
ID[p] == ID[q];

16 Ejemplo de array ID

grafo3.png 

ID = [0,0,0,0,0,0,1,0];

17 Algoritmo Quick Find

Conectados(p,q)
return id[p] == id[q]

unir(p,q):
pid = id[p]
qip = id[q]
para cada 0<= i < n:
   si (id[i] == qid):
      id[i] = pid