Quick Union (II)

1 Problema con quick-find

El problema con quick-find es al hacer la operación unir, hay que recorrer todo el array y hacer varios cambios.

2 Quick-union (primera aproximación)

Utilizamos un array ID:

• Cada componente conexa va a ser representada por un árbol.
• La componente conexa esta representada por la raíz del árbol.
• \(ID[p]\) contiene al padre en el árbol, a menos que sea la raíz, en ese caso es el mismo.

3 Quick-union (primera aproximación)

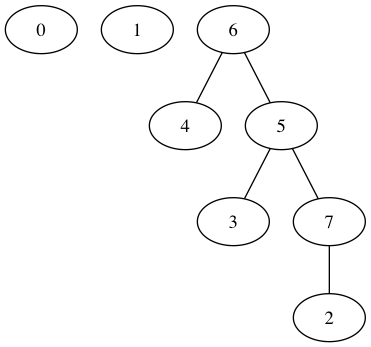
  ID = [0,1,7,5,6,6,6,5];

4 Quick-union (primera aproximación)

• Unir: solamente tenemos que cambiar la raíz del de uno de los nodos a ponerlo como hijo de la otra raíz.
• Conectados: solamente tenemos que buscar la raíz de los dos nodos y compararlos.

5 Quick-union (código)

  encontrar_raiz(n):
  mientras id[n] != n:
    n = id[n]
  return n

  Conectados(p,q):
  return encontrar_raiz(p) == encontrar_raiz(q)

  unir(p,q):
  pid = encontrar_raiz(p)
  qid = encontrar_raiz(q)
  id[pid] = qid

6 Quick-union (problemas)

• Conectados es demasiado lento.
• unir es demasiado lento.

7 Siguiente iteración

El problema es que los árboles se pueden volver muy altos.

8 Pregunta

Dada las siguientes ordenes,

  unir(0,1); unir(2,0);unir(7,2);unir(3,7);unir(4,3);

¿cómo debería hacerse el árbol para que quede de la ``mejor'' forma posible? ¿y la ``peor''?

9 Siguiente iteración

• añadir los nodos a árboles y guardar el número de nodos en el árbol en un array adicional,
• tener en cuenta el número de nodos al cambiar las raíces,
• solo hay que cambiar el número de nodos de uno de los árboles.

10 Siguiente iteración (código)

  encontrar_raiz(n):
  mientras id[n] != n:
    n = id[n]
  return n

  Conectados(p,q):
  return encontrar_raiz(p) == encontrar_raiz(q)

  unir(p,q):
  pid = encontrar_raiz(p)
  qid = encontrar_raiz(q)
  if pid != quid:
    if tamaño[pid] <tamaño[qid]:
       id[pid] = qid
       tamaño[qid] += tamaño[pid]
    else:
       id[qid] = pid
       tamaño[pid] += tamaño[qid]

11 Complejidad

• Conectados: depende de la altura de los árboles
• Unir: es constante, dadas las raíces

11.1 Teorema

Dados N objetos, y después de un número finito de inserciones, la altura de cualquiera de los árboles que se han generado es del orden logarítmico.

12 Prueba

La idea de la prueba es que los árboles solo crecen cuando son añadidos a otro árbol con más nodos.

¿Cuantos nodos tendrá, como mínimo, el nuevo árbol? ¿cuantas veces se puede repetir este proceso?

13 Podríamos parar pero….

Aquí podríamos parar pero, se puede mejorar:

• La idea es que cuando recorramos un árbol poner el padre de cada nodo a abuelo.
• Eso hace el árbol más plano.
• El análisis de este algoritmo es interesante, empezando en N objetos y realizando M uniones, hay que realizar del orden de \[N+M\log^*N\].

14 Percolación

En este problema, hay una transición de fase (es lo que se deduce del los experimentos), para N = 20:

• Cuando p es menor que 0.593, casi siempre percola.
• Cuando p es mayor que 0.593, casi nunca percola.

15 Simulación utilizando métodos Monte Carlo

• Empezar con una matriz totalmente llena.
• seleccionar a cada paso un casilla llena y liberadla.
• Si el sistema percola, contar el porcentaje de casillas libres y parar.
• En otro caso, repetir.

16 Algoritmo

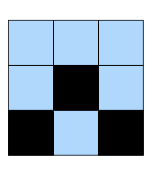
17 Algoritmo (Matriz)

18 Algoritmo (Grafo)

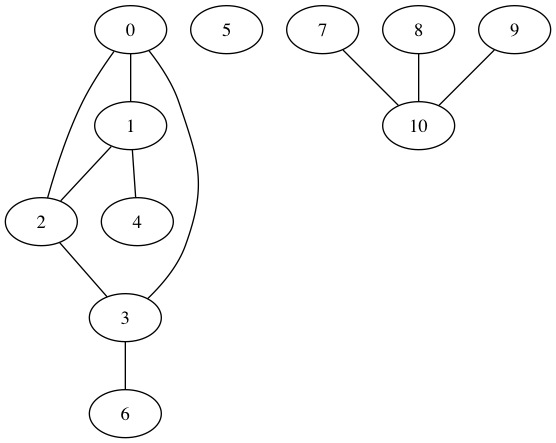
19 Pregunta

• Suponed que en el ejemplo anterior, se cambia la casilla 5 ¿que habría que hacer?

• ¿Con que linea de código se puede comprobar que el sistema percola?