Grafos

1 El problema de colorear un mapa político

Suponemos que tenemos un mapa con diferentes países y queremos pintarlos de forma que países vecinos tengan colores diferentes. ¿Cómo representamos el problema?

2 Representación (tomado del libro Algorithms de Papadimitrou et al.)

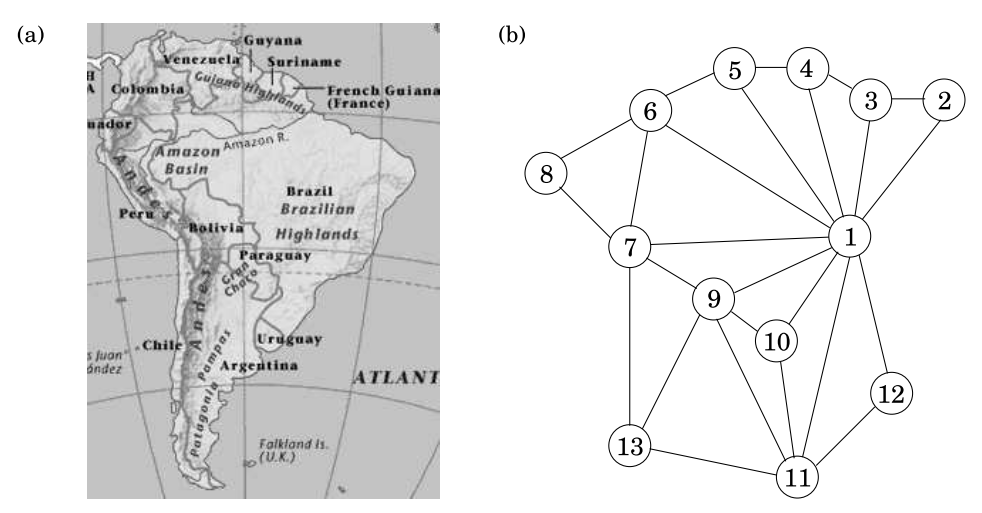
3 Representación de grafos

Los grafos consisten en un conjunto de vértices y un conjunto de aristas, G = (V, E). La representación de las aristas puede ser mediante:

Matriz de adyacencia (grafos densos).
Lista de nodos adyacentes (grafos dispersos).

4 Recorrido en grafos (tomado del libro Algorithms de Papadimitrou et al.)

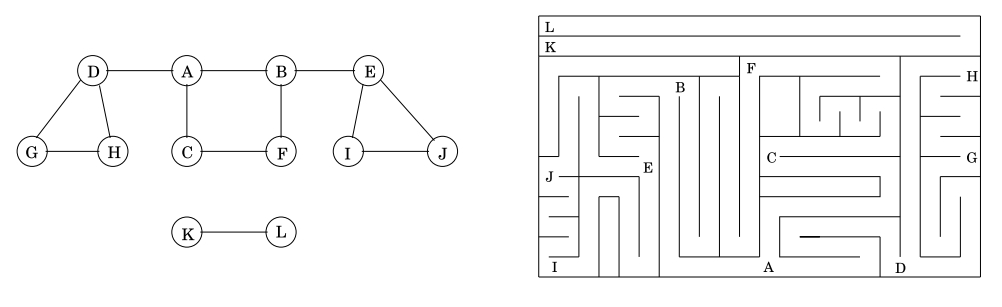
5 Algoritmo explorar

  explorar(v,G):
  visitados(v) = true
  previsit(v)
  para cada arista (v,u) en G.E:
    si no visitado(u):
      explorar(u)
  postvisit(v)

6 Algoritmo explorar

El algoritmo explorar genera una estructura de árbol no binario.

También se pueden añadir aristas de vuelta.

Almacena un array de elementos del grafo que han sido visitados.

7 Algoritmo explorar

¿Cual es el orden que da explorar?

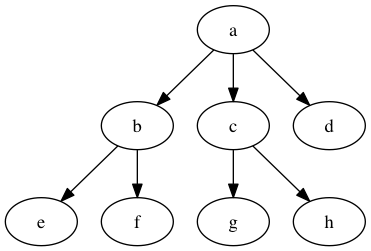
8 Algoritmo de recorrido en profundidad

  dfs(G):
  para cada v en G.V:
    visitados(v) = false
  para cada v en G.V:
    si no visitados(v):
      explorar(v)

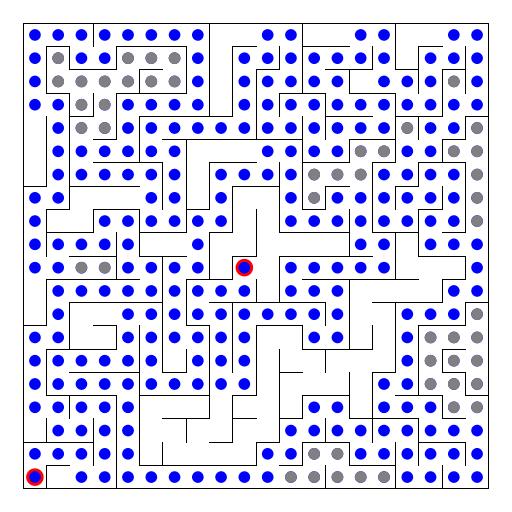
9 DFS en laberintos

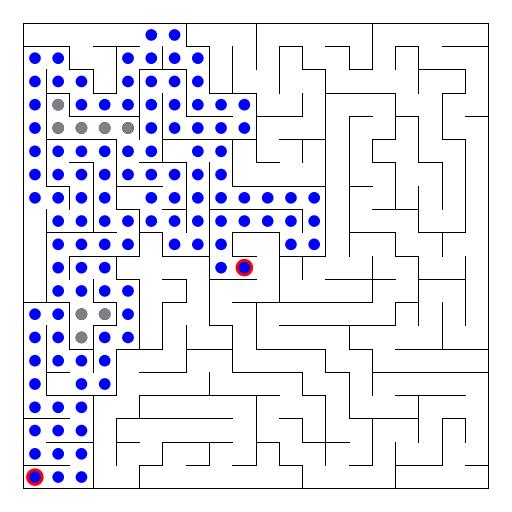
10 DFS en laberintos malos

11 Algoritmo exploración en profundidad

previsit(v):
pre[v] = clock
clock = clock + 1

postvisit(v):
post[v] = clock
clock = clock + 1

12 Algoritmo exploración en profundidad

Tipos de aristas que hay en un grafo dependiendo del árbol dfs:

Aristas del árbol. (Tree edges)
Aristas adelante. (Forward edges)
Aristas atrás. (Back edges)
Aristas cruzadas. (Cross edges)

13 Clasificar las aristas del siguiente grafo

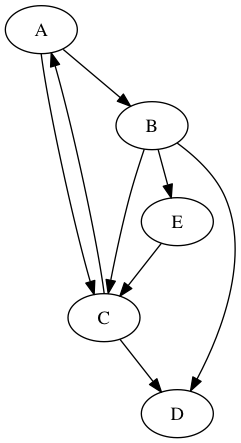
14 Pre/Post y clasificación de aristas

Tipo de arista \((u,v)\)	Relación entre los números pre/post
arista del árbol	pre[u]≤ pre[v]≤ post[v]≤ post[u]
arista adelante	pre[u]≤ pre[v]≤ post[v]≤ post[u]
arista atrás	pre[v]≤ pre[u]≤ post[u]≤ post[v]
arista cruzada	pre[v]≤ post[v]≤ pre[u]≤ post[u]