Programación dinámica
1 Repaso a caminos mínimos en DAGs
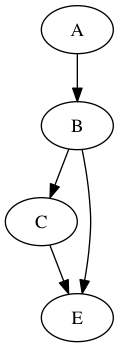
Figura 1: Dag y caminos mínimos
2 Pseudocódigo de caminos mínimos
camino_minimo(G,s):
// Inicializar todos los nodos con distancia infinita.
dist[s] = 0;
for(Nodo v:G.V)
{
for ((u,v): G.E)
{
dist[v] = min(dis[v], dist[u] + l(u,v));
}
}
3 Propiedad estrella para poder aplicar programación dinámica
Se puede, de forma fácil, ordenar los subproblemas y partir estos en problemas más pequeños de forma que la solución a los subproblemas se pueda reconstruir en una solución total.
4 El problema de la secuencia creciente más larga
Dada una secuencia de números, tenemos que encontrar la subsecuencia creciente más larga que podamos.
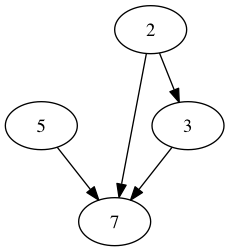
Figura 2: Ejemplo de secuencia 5,2,3,7,1 y su modelización como grafo
5 Pseudocódigo basado en programación dinámica
LIS(S):
L = new int[S.length];
for (int i=0; i<L.length; i++)
{
for(int j=0; j<i; j++)
{
if (S[i]<S[j])
L[j] = 1+ max(L[i],L[j]);
}
}
return max(L);
6 Por que no hemos hecho el algoritmo recursivo
calcular_L_i(S, i):
if (i==0)
return 1;
int L = 0;
for(int j =0; j<i; j++)
{
if (S[j]<S[i])
L = 1 + max(L, calcular_L_i(S,j));
}
return L;
7 La distancia de edición
Dada dos palabras, se define la distancia de edición como el mínimo número de ediciones que hay que hacer para transformar una palabra en la otra. Una edición puede ser cualquiera de las siguientes operaciones:
- sustituir una letra.
- borrar una letra.
- insertar una letra.
8 Algoritmo para hallar la distancia de edición
Sean \(x,y\) dos cadenas de caracteres y denotemos por \(E_{ij}\) la distancia de edición de los primeros \(i\) caracteres de \(x\) y los \(j\) primeros caracteres de \(y\). ¿Cómo podemos calcularlo?
9 Traza del algoritmo con las palabras ESTO, ROPA.
| i/j | R | O | P | A |
|---|---|---|---|---|
| E | 1 | 2 | 3 | 4 |
| S | 2 | 2 | 3 | 4 |
| T | 3 | 3 | 3 | 4 |
| O | 4 | 3 | 4 | 4 |
10 El DAG oculto
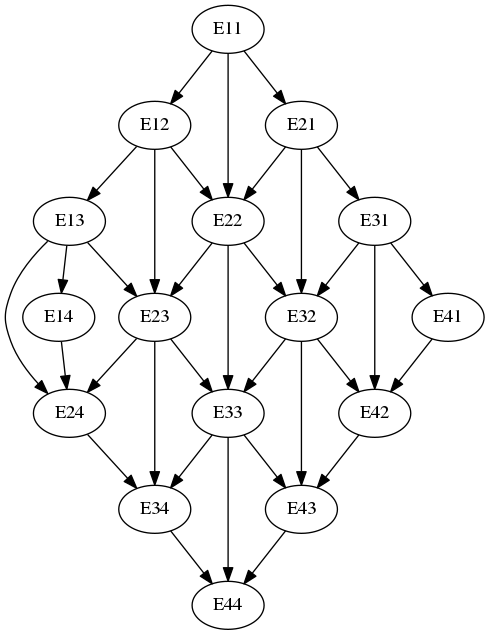
Figura 3: DAG oculto
11 El DAG oculto
El DAG oculto se genera a partir de los subproblemas. Las llamadas que se hacen y los problemas que se resuelven hacen que la solución sea más efectiva o menos.
12 Computación genómica
Las cadenas de ADN pueden ser vistas como cadenas de texto con solo cuatro símbolos \(A,C,T,G\).
13 Aplicaciones a la computación genómica
- Hallar la función de un gen.
- Secuenciar el genoma humano.
- Reconstruir la historia evolutiva de una especie.
14 Reconstruyendo el genoma
- El orden de los trozos que recuperamos se ha perdido.
- Se toma aproximadamente un billón de trozos de cadenas de longitud cien.
- Gracias al proyecto genoma humano, ahora es posible reconstruir el genoma.
15 Reconstruyendo el genoma
- Referencia: CTAGCAATGACAGGACATTACATGTCCA
- Secuencia alineada: GCAATGACAGGACA ACATGTC
- uno de los billones de trozos: GCAATGAGAGGACAACATGTC
16 Degeneración macular
La degeneración macular es una enfermedad que empieza a los treinta años y que deriva en que la zona central de la visión es muy borrosa.
17 Método para encontrar cadenas de texto
- Suffix trie
- Suffix tree
18 Ejemplo de suffix trie
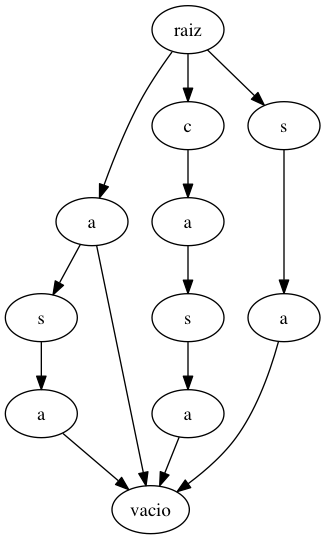
Figura 4: Suffix trie de casa