Programación dinámica II
1 El problema de la mochila
Suponemos que tenemos una mochila donde podemos meter hasta 15 kilos, y tenemos los siguiente items:
| Item | peso | valor |
|---|---|---|
| 1 | 13 | 50 |
| 2 | 11 | 40 |
| 3 | 8 | 35 |
| 4 | 7 | 30 |
| 5 | 3 | 15 |
| 6 | 2 | 5 |
2 Dos versiones del problema de la mochila
- Con repetición.
- Sin repetición.
3 El problema de la mochila con repetición
Sea \(K(W)\) el valor óptimo de la mochila con restricción de peso \(W\), entonces se tiene: \[ K(W) = \max\{K(W-w_i) + v_i\}. \]
4 Pregunta
El dag del problema de la mochila, ¿a qué problema es equivalente en los DAGs?
5 El problema de la mochila sin repetición
Se define la siguiente cantidad: \[ K(W,j) = \text{máximo valor utilizando solamente los items de 1 a j sin repetir}. \]
6 El problema de la mochila sin repetición
\[ K(W,j) = \max\{K(W-w_j,j-1)+ v_j,K(W,j-1)\}. \]
7 Interludio: Memoization
Memoization es una técnica que, lo que hace es guardar en memoria resultados intermedios para no tener que calcularlos.
Knapsack(w): if w in hash_table: return hash_table(w) K(w) = max(K(w-w_i)+ v_i: w_i<=w) insert w in hash_table return K(w)
8 Interludio: Memoization
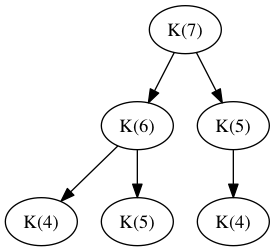
Figura 1: Árbol parcial de llamadas
9 Pregunta
Suponer que, nos dan un grafo y nos piden que hallemos los caminos más cortos con la restricción de que los cáminos tienen que tener menos de \(\ell\) aristas, rellenar la siguiente propiedad: \[ dist(v,i) = \dots \] ¿Cúal es el valor que debemos poner con \(dist(v,0)\)?
10 Hallar cáminos mínimos entre cualquier par de vértices
Idea:
- Calcular los cáminos mínimos sólo utilizando ejes directos.
- Ir permitiendo nodos intermedios a cada paso.
- Cuando todos los nodos sean permitidos como intermedios, hemos acabado.
11 El algoritmo de Floyd-Warshall
Definid \(dist(i,j,k)\) sea la distancia mínima de \(i\) a \(j\) pasando por nodos intermedios \(1,\ldots, k\). Ahora, la recursión es \[ dist(i,j,k) = \min\{dist(i,k,k-1)+dist(k,j,k-1),dist(i,j,k-1)\} \]
12 Cantidad de memoria necesaria
La cantidad de memoria necesaria es a lo sumo:
- La memoria es, a lo sumo, proporcional al tamaño del DAG.
- Muchas veces, se puede reducir porque cuando solo es necesario
guardar los subproblemas necesarios.
- En Floyd-Warshall la memoria necesaria es \(O(|V|^2)\)
- Para hallar la distancia de edición es proporcional a la longitud de la palabra más corta.
13 El problema del conjunto independiente
Dado un grafo, se llama un conjunto independiente es un conjunto de nodos que no tienen un eje entre ellos.
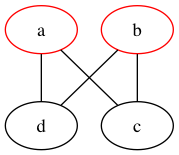
Figura 2: Ejemplo de grafo con un conjunto independiente
14 El problema del conjunto independiente (en árboles)
Sea \(I(u)\) el tamaño máximo de un conjunto independiente, entonces tenemos:
- el tamaño del conjunto independiente es el mismo que el máximo de los conjuntos independientes de los hijos.
- el tamaño del conjunto independiente es uno más que el máximo de los conjuntos independientes de los nietos.
15 El problema del conjunto independiente (en árboles)
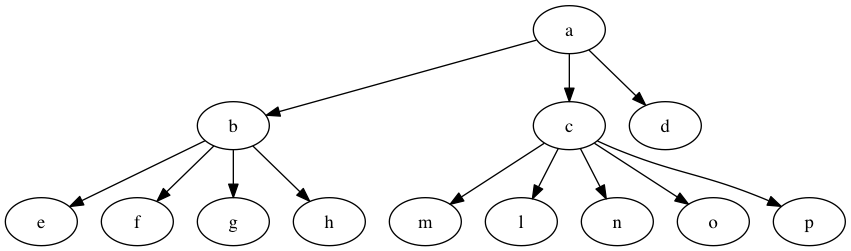
Figura 3: Árbol para calcular el tamaño máximo