Ciclos y grafos acíclicos

1 Definición de ciclos

ejemplo_ciclo.png

Figura 1: Figura con ciclos

1.1 Definición de camino

Un camino en un grafo es una lista de nodos de forma que dos nodos consecutivos son adyacentes. Utilizaremos la siguiente notación: \[ v_0\mapsto v_1\mapsto\ldots v_n. \]

1.2 Definición de ciclo

Un ciclo es un camino donde el vértice de inicio y el final son iguales.

2 ¿Cómo podemos saber si un grafo tiene ciclos?

2.1 Propiedad

Un grafo dirigido tiene ciclos si y solamente si realizando el algoritmo DFS aparecen aristas atrás.

3 Ciclos

prueba.png

Figura 2: Figura con ciclos

4 DAG (Direct Acyclic Graphs)

Los grafos directos acíclicos son muy utilizados, modelan:

  • relaciones de causalidad,
  • cadenas de trabajos,
  • parentescos,
  • preguntas y respuestas.

5 Propiedades de los DAGs

dag.png

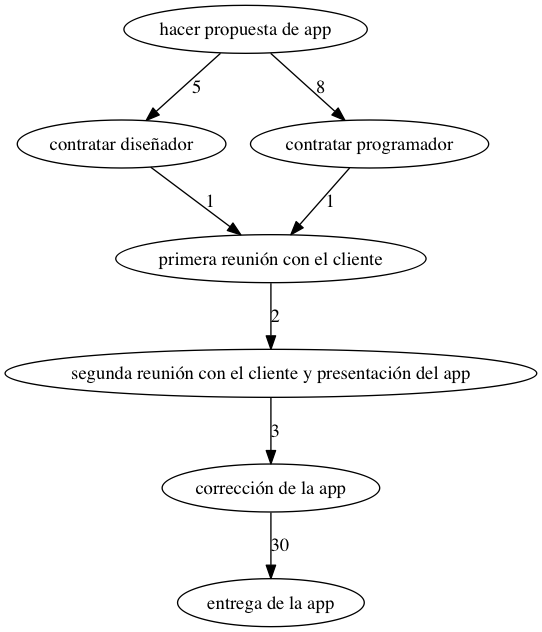
Figura 3: Ejemplo de DAG

  • En los DAGs hay, al menos, una fuente y un sumidero.
  • Un DAG admite una linearización.
  • En un DAG, cada eje lleva a nodos con menor valor post.

6 ¿En que orden hay que ponerse el equipamiento?

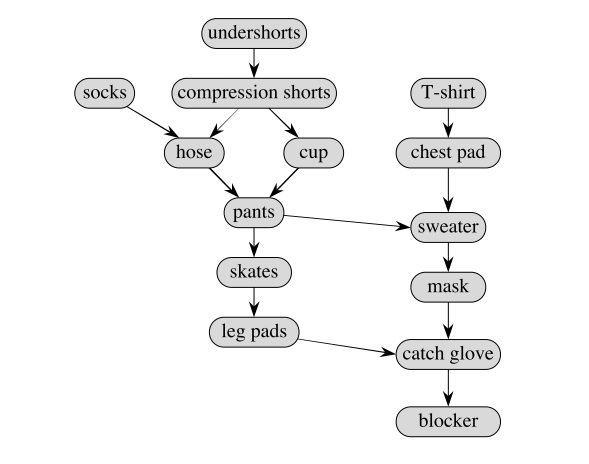
hockey.png

Figura 4: Tomada del libro Unlocked algorithms de T. Cormen (capítulo 5).

7 Grafos con pesos en las aristas

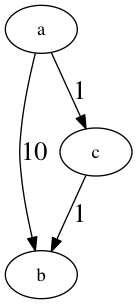
pesos.png

Figura 5: Grafo con pesos

8 Otro ejemplo de ordenación lineal

tareas.png

9 Camino crítico en un grafo

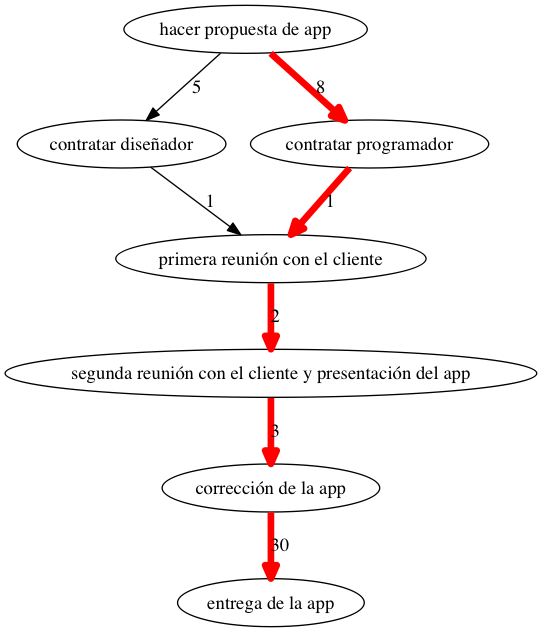
tareas1.png

10 Camino crítico

El camino crítico en un grafo es el camino cuya suma de longitudes de aristas es máxima entre todos los posibles caminos.

11 Camino mínimo

El camino mínimo entre dos vértices u,v es cualquier con longitud mínima entre u y v.

12 Caminos mínimos en DAGs

  • Linearizar el DAG.
  • Llevar dos arrays distancia y predecesor
  • Recorrer los vertices en el orden dado por linearizar e ir actualizando tanto el array de distancias y el predecesor

13 Problemas de DFS

dfs.png

14 BFS (Busqueda en anchura)

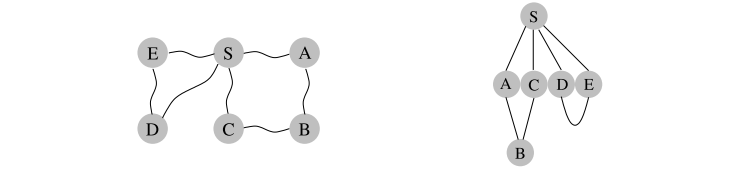
modelo_fisico.png

Imagen tomada de Algorithms ( Papadimitriou, C. H. et al)

15 BFS (Busqueda en anchura)

  BFS(G,s):
  for(int u: G.V):
    distancia[u]=Double.Infinity;
  distancia[s] = 0;
  Q = Queue(s);
  while !Q.isEmpty(){
    u = Q.poll();
    for((u,v): G.E){
      if(distancia[v] == Double.Infinity)
      {
        Q.push(v);
        distancia[v]=distancia[u] + 1;
      }

    }
  }

16 BFS con longitudes de aristas enteras

BFS_pesos.png

Figura 10: Dos grafos equivalentes para BFS

17 BFS con longitudes de aristas enteras

  1. Elegir un nodo de inicio s.
  2. Poner la alarma de ese nodo a 0.
  3. Repetir mientras haya alarmas.
    1. Denotemos T el tiempo de la siguiente alarma y nos despertamos en u.
    2. Ponemos la distancia de u a T.
    3. A cada uno de sus vecinos le asignamos el menor valor entre la alarma que da T mas la longitud de la arista que los une o la que tienen.

18 El algoritmo de Dijkstra

El algoritmo de Dijkstra implementa el sistema de alarmas con una cola de prioridad que tiene las siguientes operaciones:

  • Insert
  • Decrease-key
  • Delete-min
  • Make-queue

19 El algoritmo de Dijkstra

  update(u,v):
  if (dist[v] > dist(u) + l(u,v))
  {
      dist[v] = dist(u) + l(u,v);
      prev[v] = u;
      Decrease-key(H,v);
  }

20 El algoritmo de Dijkstra

  dijkstra (G, l, s):
  for (v: V)
  {
  dist[v] = Infinity;
  prev[v] = nil;
  }
  dist[s] = 0;
  H = makequeue(s); // Hacer la cola de prioridad
  while(!H.empty())
  {
    u = H.Delete-min();
    for ((u,v): E)
    {
    update(u,v);
    }

  }

21 El algoritmo de Dijkstra con pesos negátivos

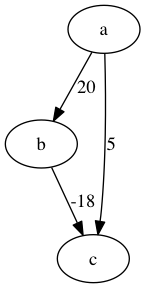
pesos_negativos.png

Figura 11: Grafo con pesos negativos

22 El algoritmo de Bellman-Ford


  BellmanFord (G, l, s):
  for (v: V)
  {
  dist[v] = Infinity;
  prev[v] = nil;
  }
  dist[s] = 0;
  for(v:V)
  {
    for(e:E)
    {
      update(e);
    }
  }