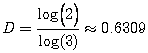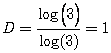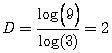Propiedades
Veamos ahora alguna propiedad de este curioso conjunto. Para ello rellena la siguiente tabla
| Etapa | Número de segmentos | Longitud de cada segmento | Suma de las longitudes de todos los segmentos |
| 0 | 1 | 1 unidad | 1 unidad |
| 1 | 2 | ||
| 2 | 4 | ||
| 3 | 8 | ||
| ... | |||
| n |
Pregunta: ¿Qué observas en relación a la longitud de este conjunto?
Algunas propiedades de este conjunto son las siguientes:
- Su longitud es cero, pero tiene tantos puntos como toda la recta real.
- Es un conjunto totalmente disconexo: entre cada dos puntos siempre hay infinitos puntos que no pertenecen al conjunto.
- Si tomamos A=0 y B=1 este conjunto está formado por aquellos puntos del intervalo unidad cuya expresión en base 3 no contienen el dígito 1.
Dimensión fractal (dimensión de autosemejanza)
Además de la propiedad de autosimilitud los fractales poseen otra propiedad que hace referencia a su irregularidad. Se denomina dimensión fractal y normalmente es un número fraccionario.
Si observamos el conjunto de Cantor, vemos que en cada paso se reduce la longitud 1/3. Felix Hausdorff definió en 1919 un nuevo concepto de dimensión que Mandrelbrot tomó para caracterizar los fractales. Así, si un todo se puede descomponer en N partes que se obtienen mediante una homotecia de razón R entonces la figura se dice que tiene una dimensión fractal dada por la expresión:
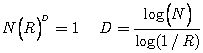
Por ejemplo, un segmento tiene dimensión fractal 1
|
|
R=1/3, N=3
|
Un cuadrado tiene dimensión fractal 2 ya que
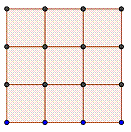 |
R=1/3, N=9
|
Pregunta: Y ¿un cubo dividido en 27 partes?
Observa que: El conjunto de Cantor tiene una dimensión fraccionaria entre 0 y 1 (es algo más que un punto pero menos que un segmento). Su dimensión se puede calcular con la fórmula anterior teniendo en cuenta que N=2 y R=1/3