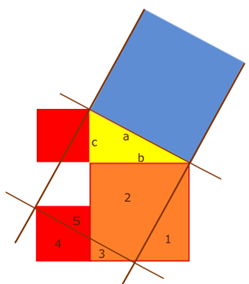
| El teorema de Pitágoras afirma que, dado un triángulo rectángulo, el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. | |||||||||||
|
|
Si haces clic sobre el siguiente botón puedes ver distintos puzzles que demuestran este resultado.
En la siguiente descripción de los puzzles se considera siempre un triángulo rectángulo, T, de catetos b y c e hipotenusa a. Para una descripción más detallada de cómo obtener las piezas de los distintos puzzles puedes hacer clic en el siguiente botón:
|
||||||||||
|
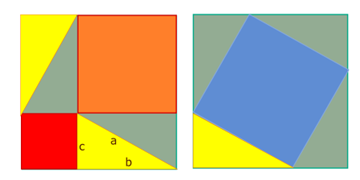
Puzzle 1: Pitágoras de Samos (s. VI a. C.)
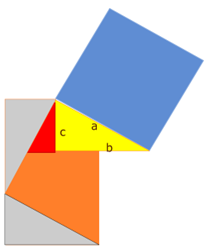
Puzzle 2: Thabit Ibn Qurra (826-901)
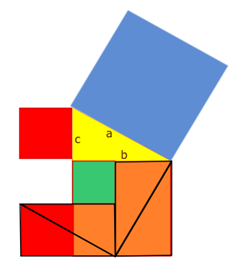
Puzzle 3: Bhâskara (1114-1185)
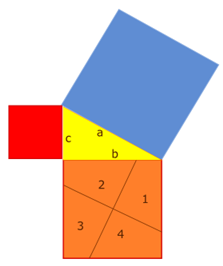
Puzzle 4: Demostración de Henry Perigal (1801-1898)
Puzzle 5: Demostración de Fréderic Ozanam (1813-1853)
|
|||||||||||